Exploring Graph Algorithms

Graphs are essential data structures in computer science that represent relationships between different entities. They effectively model complex connections, making them applicable in various fields, from social networks to transportation systems. In this post, we will explore two fundamental graph traversal algorithms: Breadth-First Search (BFS) and Depth-First Search (DFS).

---

Understanding Graphs

Graphs are made up of nodes (also known as vertices) that are connected by edges. They can be categorized into different types:

• Directed Graphs: Edges have a direction (e.g., one-way streets).
• Undirected Graphs: Edges don’t have direction (e.g., mutual friendships).
• Cyclic Graphs: Contain cycles where you can traverse a path and return to the starting node.

Visual Examples

Directed Graph

Edges have a direction, meaning they point from one node to another. For example, in a graph representing prerequisites for courses, an edge from A to B signifies that course A must be completed before course B

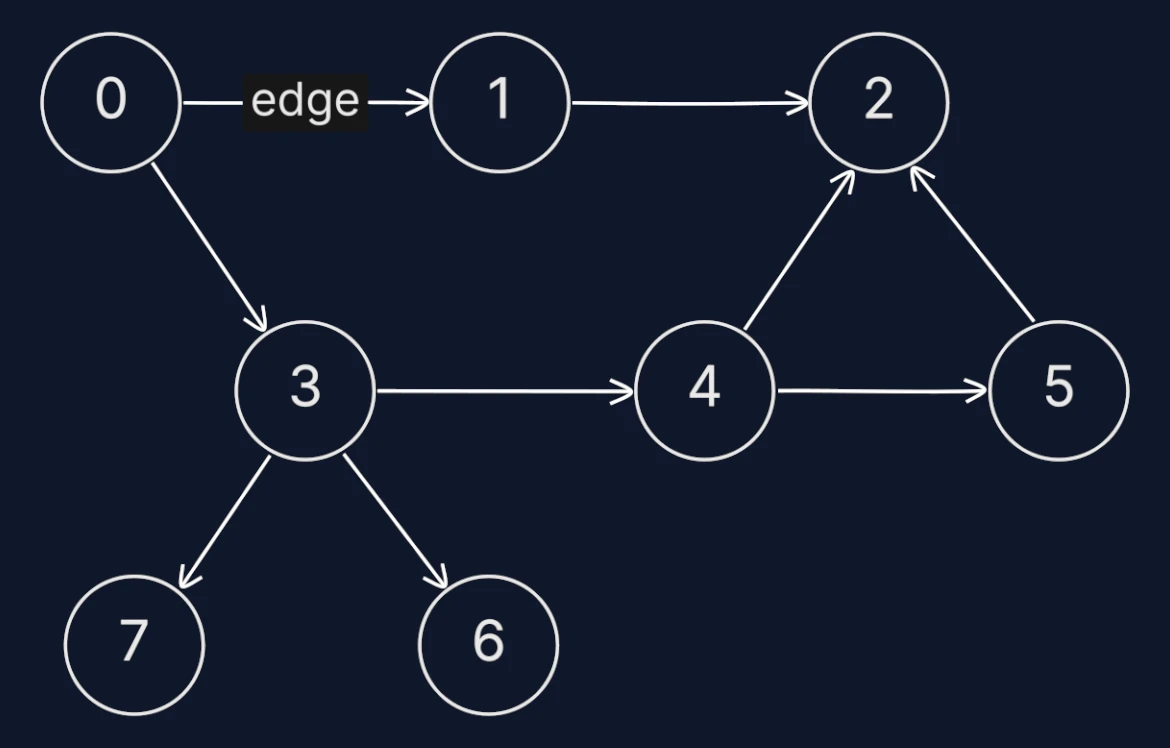
var adjacencyList = [][]int{
   {0,1},
   {0,3},
   {1,2},
   {3,4},
   {3,6},
   {3,7},
   {4,2},
   {4,5},
   {5,2}
}

Undirected Graph

Edges have no direction, implying a mutual connection between nodes. For instance, in a graph modeling friendships, an edge between A and B means that A and B are friends.

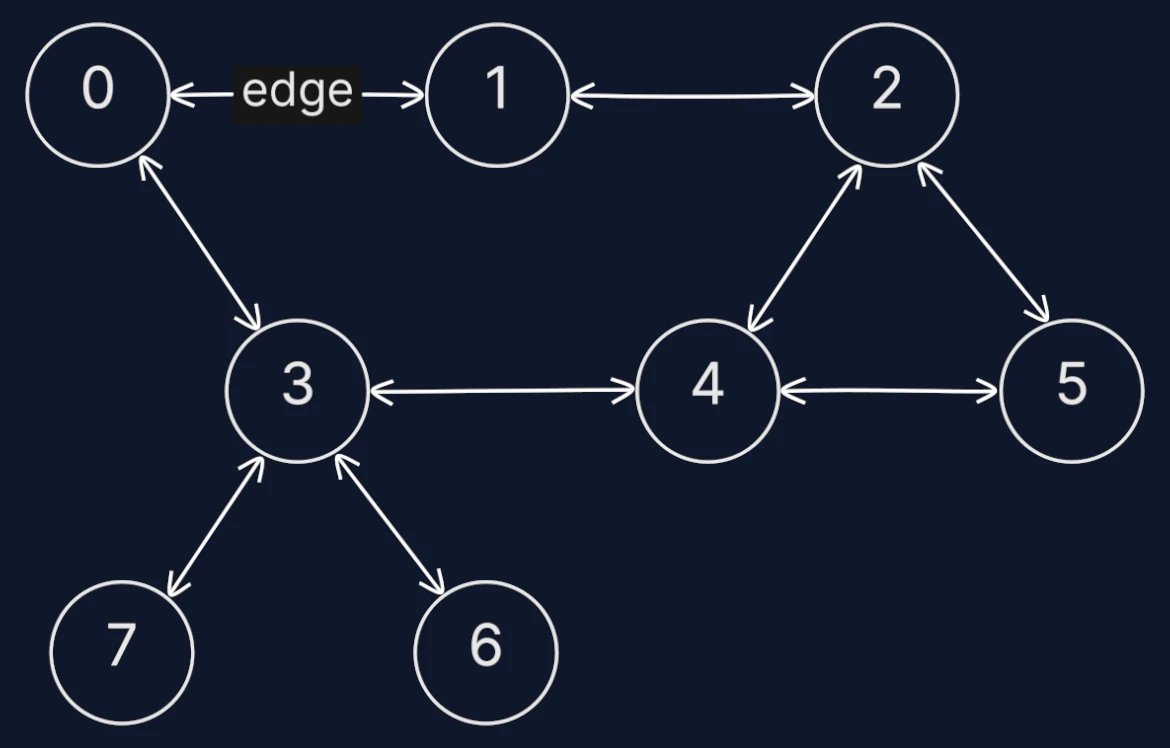
var adjacencyList = [][]int{
   {0, 1}, {1, 0},
   {0, 3}, {3, 0},
   {1, 2}, {2, 1},
   {3, 4}, {4, 3},
   {3, 6}, {6, 3},
   {3, 7}, {7, 3},
   {4, 2}, {2, 4},
   {4, 5}, {5, 4},
   {5, 2}, {2, 5},
} 

Cyclic Graph

Contain cycles, where a path can start and return to the same node without repeating an edge. Cycles are often seen in road networks where circular routes exist.

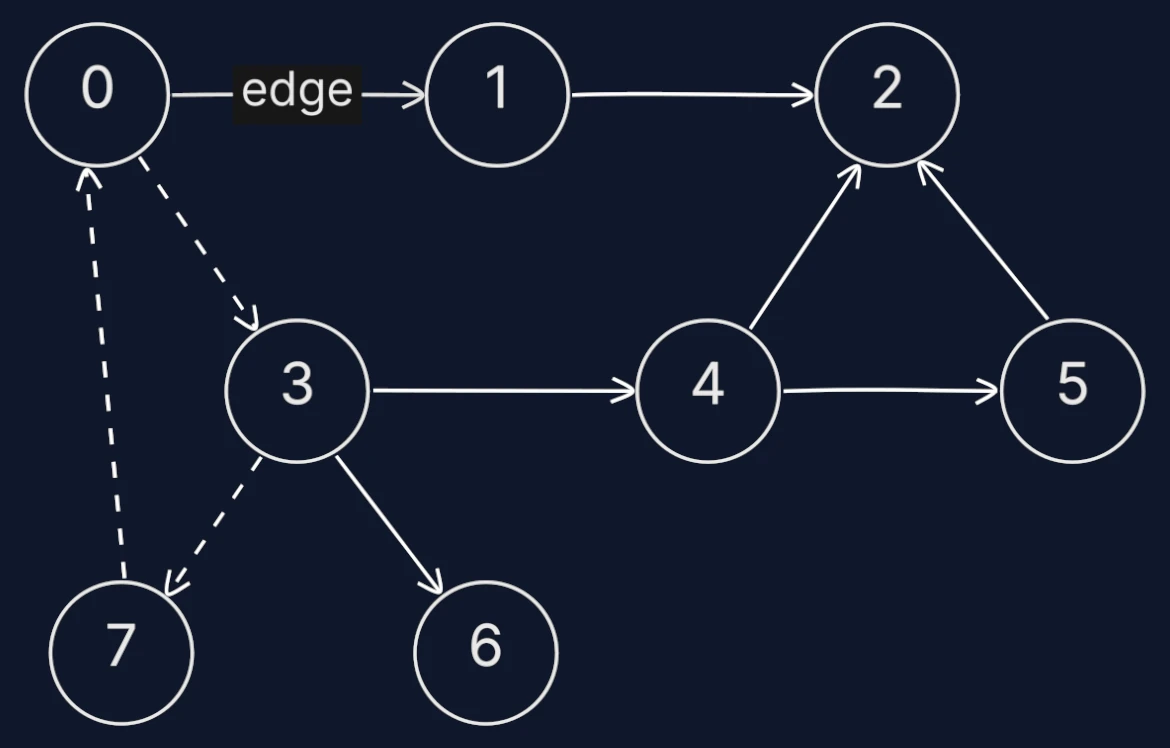
var adjacencyList = [][]int{
   {0,1},
   {0,3}, {3, 7}, {7, 0}
   {1,2},
   {3,4},
   {3,6},
   {3,7},
   {4,2},
   {4,5},
   {5,2}
} 

These structures form the foundation for graph algorithms.

---

Graph Representation

Graphs can be represented using different data structures, each with its own pros and cons:

Adjacency Matrix

An adjacency matrix is a 2D array where each cell (i, j) indicates the presence or absence of an edge between nodes i and j.

Example:

For an undirected graph:

• Advantages:
  • Easy to implement and understand.
  • Efficient for dense graphs where most nodes are connected.
• Disadvantages:
  • Consumes more memory for sparse graphs.
  • Checking for neighbors requires scanning the entire row.

Adjacency List

An adjacency list represents the graph as a map or list where each node points to a list of its neighbors.

For the same undirected graph:

• Advantages:
  • Efficient memory usage for sparse graphs.
  • Faster to iterate through neighbors.
• Disadvantages:
  • Slightly more complex to implement.
  • Less efficient for dense graphs compared to an adjacency matrix.

Which to Use?

• Use an adjacency matrix for dense graphs where edge presence needs to be checked frequently.
• Use an adjacency list for sparse graphs with frequent traversal operations like BFS or DFS.

---

Breadth-First Search (BFS)

BFS explores a graph level by level, starting from a given node. It uses a queue to keep track of nodes to visit next.

Algorithm

1. Start with a source node.
2. Enqueue the source node and mark it as visited.
3. While the queue is not empty:
   • Dequeue a node.
   • Visit all its unvisited neighbors and enqueue them.

Go and Typescript Implementation

Here’s a BFS implementation for an undirected graph:

package main

import (
 "container/list"
 "fmt"
)

type Graph struct {
 adjacencyList map[string][]string
}

func NewGraph() *Graph {
 return &Graph{
  adjacencyList: make(map[string][]string),
 }
}

func (g *Graph) AddEdge(v1, v2 string) {
 g.adjacencyList[v1] = append(g.adjacencyList[v1], v2)
 g.adjacencyList[v2] = append(g.adjacencyList[v2], v1) // Undirected graph
}

func (g *Graph) BFS(start string) {
 visited := make(map[string]bool)
 queue := list.New()

 visited[start] = true
 queue.PushBack(start)

 for queue.Len() > 0 {
  current := queue.Remove(queue.Front()).(string)
  fmt.Println(current)

  for _, neighbor := range g.adjacencyList[current] {
   if !visited[neighbor] {
    visited[neighbor] = true
    queue.PushBack(neighbor)
   }
  }
 }
}

func main() {
 graph := NewGraph()
 graph.AddEdge("A", "B")
 graph.AddEdge("A", "C")
 graph.AddEdge("B", "D")
 graph.AddEdge("C", "D")
 graph.BFS("A")
}

class Graph {
   private adjacencyList: Map<string, string[]> = new Map();

   addEdge(vertex1: string, vertex2: string) {
      if (!this.adjacencyList.has(vertex1)) this.adjacencyList.set(vertex1, []);
      if (!this.adjacencyList.has(vertex2)) this.adjacencyList.set(vertex2, []);
      this.adjacencyList.get(vertex1)!.push(vertex2);
      this.adjacencyList.get(vertex2)!.push(vertex1); // Undirected graph
   }

   bfs(start: string) {
      const queue: string[] = [start];
      const visited: Set<string> = new Set();

      visited.add(start);

      while (queue.length > 0) {
         const current = queue.shift()!;

         for (const neighbor of this.adjacencyList.get(current) || []) {
            if (!visited.has(neighbor)) {
               visited.add(neighbor);
               queue.push(neighbor);
            }
         }
      }
   }
}

const graph = new Graph();
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("B", "D");
graph.addEdge("C", "D");
graph.bfs("A");

---

Depth-First Search (DFS)

DFS dives deep into the graph, exploring as far as possible along one branch before backtracking. It can be implemented recursively or iteratively using a stack.

Algorithm

1. Start with a source node.
2. Visit the node and mark it as visited.
3. Recursively visit all its unvisited neighbors.

Typescript Implementation

Here’s a recursive DFS implementation:

package main

import "fmt"

type Graph struct {
 adjacencyList map[string][]string
}

func NewGraph() *Graph {
 return &Graph{
  adjacencyList: make(map[string][]string),
 }
}

func (g *Graph) AddEdge(v1, v2 string) {
 g.adjacencyList[v1] = append(g.adjacencyList[v1], v2)
 g.adjacencyList[v2] = append(g.adjacencyList[v2], v1) // Undirected graph
}

func (g *Graph) DFS(start string, visited map[string]bool) {
 if visited[start] {
  return
 }
 visited[start] = true
 fmt.Println(start)

 for _, neighbor := range g.adjacencyList[start] {
  g.DFS(neighbor, visited)
 }
}

func main() {
 graph := NewGraph()
 graph.AddEdge("A", "B")
 graph.AddEdge("A", "C")
 graph.AddEdge("B", "D")
 graph.AddEdge("C", "D")

 visited := make(map[string]bool)
 graph.DFS("A", visited)
}

class GraphDFS {
   private adjacencyList: Map<string, string[]> = new Map();

   addEdge(vertex1: string, vertex2: string) {
      if (!this.adjacencyList.has(vertex1)) this.adjacencyList.set(vertex1, []);
      if (!this.adjacencyList.has(vertex2)) this.adjacencyList.set(vertex2, []);
      this.adjacencyList.get(vertex1)!.push(vertex2);
      this.adjacencyList.get(vertex2)!.push(vertex1); // Undirected graph
   }

   dfs(start: string, visited: Set<string> = new Set()) {
      if (visited.has(start)) return;
      visited.add(start);
      console.log(start);

      for (const neighbor of this.adjacencyList.get(start) || []) {
         this.dfs(neighbor, visited);
      }
   }
}

const graphDFS = new GraphDFS();
graphDFS.addEdge("A", "B");
graphDFS.addEdge("A", "C");
graphDFS.addEdge("B", "D");
graphDFS.addEdge("C", "D");
graphDFS.dfs("A");

BFS vs. DFS

Feature	BFS	DFS
Approach	Level-by-level traversal	Depth-first traversal
Data Structure	Queue	Stack (or recursion)
Use Cases	Shortest path, Network exploration	Topological sorting, Cycle detection

---

Practical Applications

BFS:

• Finding the shortest path in unweighted graphs.
• Crawling social networks.
• Broadcasting messages in networks, such as in multiplayer online games.
• Solving puzzles like the 8-puzzle or sliding tile games.

DFS:

• Detecting cycles in graphs.
• Solving mazes or puzzles where paths need exploration, such as the N-Queens problem.
• Performing topological sorting in dependency graphs.
• Analyzing connectivity in networks, like finding bridges or articulation points in a graph.

Daily Use Cases:

• Route Optimization: Use BFS to find the shortest route between locations on a map or DFS to explore all possible routes.
• Friend Recommendations: In social networks, BFS can help identify mutual friends or suggest connections.
• Task Scheduling: DFS is used to analyze dependencies among tasks, ensuring they’re executed in the correct order.
• Web Crawling: BFS ensures that search engines can systematically explore all links on a website.
• Game Development: Use DFS for generating mazes or BFS for finding the shortest path in game maps.
• Network Troubleshooting: Analyze the connectivity or detect loops in network configurations using DFS.

Interview Benefits:

• As a developer, mastering BFS and DFS can be a significant advantage in technical interviews. Here’s how:
• Common Interview Questions: Problems involving graphs, trees, or networks often require BFS or DFS. Examples include finding the shortest path, detecting cycles, or traversing a maze.
• Problem-Solving Framework: These algorithms provide structured approaches to explore solutions, making them versatile tools for tackling a range of interview problems.
• Algorithmic Thinking: Understanding BFS and DFS improves your ability to think algorithmically, which is a critical skill for solving complex problems.
• Practical Demonstration: Implementing these algorithms during an interview showcases your coding proficiency, understanding of data structures, and problem-solving skills.
• Transferable Knowledge: Many advanced algorithms, such as Dijkstra's or A*, build upon BFS and DFS concepts.

---

Pros and Cons

Breadth-First Search (BFS)

Pros:

• Guarantees shortest path in unweighted graphs. Explores all nodes at the current depth before moving deeper, making it ideal for level-order processing.
• Useful for finding connected components in an unweighted graph.

Cons:

• Higher memory usage due to the queue.
• Can be slower if the solution is far from the source node.

Depth-First Search (DFS)

Pros:

• Lower memory usage (stack depth).
• Useful for problems requiring exploration of all paths.
• Can be adapted for applications like topological sorting and detecting cycles.

Cons:

• Does not guarantee shortest path.
• Can get stuck exploring deep paths in cyclic graphs without proper handling (e.g., visited nodes).
• May require backtracking, which can increase the time complexity in certain scenarios.

---

Summary

Graphs are versatile tools, and BFS and DFS are essential for navigating them. BFS excels in finding shortest paths, while DFS is ideal for comprehensive exploration. By mastering these algorithms, you unlock the ability to solve a wide range of real-world problems.

As always, take care in that coding journey, and I’ll catch you next time! 🤖